Operations on Signals

This section describes the operations that can be performed on signals.

See also

Processing Signals for more information on signal processing features, or Analysis features on Signals for information on analysis features on signals.

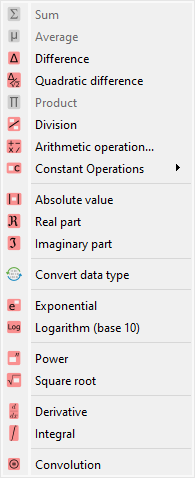
Screenshot of the “Operations” menu.

When the “Signal Panel” is selected, the menus and toolbars are updated to provide signal-related actions.

The “Operations” menu allows you to perform various operations on the selected signals, such as arithmetic operations, peak detection, or convolution.

Operations with a constant

Create a new signal which is the result of a constant operation on each selected signal:

Operation	Description
Addition	\(y_{k} = y_{k-1} + c\)
Subtraction	\(y_{k} = y_{k-1} - c\)
Multiplication	\(y_{k} = y_{k-1} \times c\)
Division	\(y_{k} = \dfrac{y_{k-1}}{c}\)

Basic arithmetic operations

Operation	Description
Sum	\(y_{M} = \sum_{k=0}^{M-1}{y_{k}}\)
Difference	\(y_{2} = y_{1} - y_{0}\)
Product	\(y_{M} = \prod_{k=0}^{M-1}{y_{k}}\)
Division	\(y_{2} = \dfrac{y_{1}}{y_{0}}\)
Inverse	\(y_{2} = \dfrac{1}{y_{1}}\)
Exponential	\(y_{2} = \exp(y_{1})\)
Logarithm (base 10)	\(y_{2} = \log_{10}(y_{1})\)

Convolution and Deconvolution

Operation	Implementation
Convolution	Based on scipy.signal.convolve
Deconvolution	Frequency domain deconvolution

Absolute value and complex signal operations

Operation	Description
Absolute value	\(y_{k} = |y_{k-1}|\)
Phase (argument)	sigima.proc.signal.phase()
Combine with phase	Consider current signal as the module and allow to select a signal representing the phase to merge them in a complex signal sigima.proc.signal.complex_from_magnitude_phase()
Real part	\(y_{k} = \Re(y_{k-1})\)
Imaginary part	\(y_{k} = \Im(y_{k-1})\)
Combine with imaginary part	Consider current signal as the real part and allow to select a signal representing the imaginary part to merge them in a complex signal sigima.proc.signal.complex_from_real_imag()

Data type conversion

The “Convert data type” action allows you to convert the data type of the selected signals.

Note

Data type conversion relies on numpy.ndarray.astype() function with the default parameters (casting=’unsafe’).

Statistics between signals

Create a new signal which is the result of a statistical operation on each point of the selected signals:

Operation	Description
Average	\(y_{M} = \dfrac{1}{M}\sum_{k=0}^{M-1}{y_{k}}\)
Standard Deviation	\(y_{M} = \sqrt{\dfrac{1}{M}\sum_{k=0}^{M-1}{(y_{k} - \bar{y})^{2}}}\)

Other mathematical functions

Function	Description
Power	\(y_{k} = y_{k}^{n}\)
Square root	\(y_{k} = \sqrt{y_{k}}\)
Derivative	Based on numpy.gradient
Integral	Based on scipy.integrate.cumulative_trapezoid
Assemble signals into image	Create a 2D image by assembling selected 1D signals as rows or columns, with optional normalization.