Opérations sur les images#

Cette section décrit les opérations qui peuvent être effectuées sur les images.

Voir aussi

Traitement des images pour plus d’informations sur les fonctionnalités de traitement d’image, ou Analyse sur les images pour des informations sur les fonctionnalités d’analyse des images.

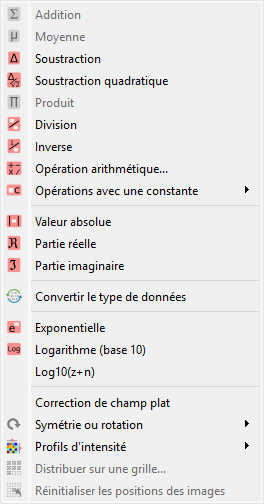
../../_images/i_operation.png — Capture d’écran du menu « Opérations ».#

Lorsque le « Panneau Image » est sélectionné, les menus et barres d’outils sont mis à jour pour fournir les actions liées aux images.

Le menu « Opérations » permet d’effectuer diverses opérations sur l’image ou le groupe d’images courant. Il permet également d’extraire des profils, de distribuer des images sur une grille, ou de redimensionner des images.

Opérations avec une constante#

Crée une image à partir d’une opération avec une constante sur chaque image sélectionnée :

Opération	Equation
Addition	\(z_{k} = z_{k-1} + conv(c)\)
Soustraction	\(z_{k} = z_{k-1} - conv(c)\)
Multiplication	\(z_{k} = conv(z_{k-1} \times c)\)
Division	\(z_{k} = conv(\dfrac{z_{k-1}}{c})\)

où \(c\) est la valeur constante et \(conv\) est la fonction de conversion qui gère la conversion du type de données (en conservant le même type de données que l’image d’entrée).

Opérations arithmétiques de base#

Les opérations arithmétiques sont effectuées pixel par pixel entre les images sélectionnées.

Opération	Description
Somme	\(z_{M} = \sum_{k=0}^{M-1}{z_{k}}\)
Soustraction	\(z_{2} = z_{1} - z_{0}\)
Produit	\(z_{M} = \prod_{k=0}^{M-1}{z_{k}}\)
Division	\(z_{2} = \dfrac{z_{1}}{z_{0}}\)
Inverse	\(z_{2} = \dfrac{1}{z_{1}}\)
Exponentielle	\(z_{2} = \exp(z_{1})\)
Logarithme (base 10)	\(z_{2} = \log_{10}(z_{1})\)

Fonctions mathématiques de base#

Fonction	Description
Exponentielle	\(z_{k} = \exp(z_{k})\)
Logarithme (base 10)	\(z_{k} = \log_{10}(z_{k})\)
Log10(z+10)	\(z_{k} = \log_{10}(z_{k}+n)\) (utile si le fond de l’image est nul)

Convolution et Déconvolution#

Opération	Implémentation
Convolution	Basée sur scipy.signal.convolve
Déconvolution	Déconvolution dans le domaine fréquentiel

Valeur absolue et opérations sur les images complexes#

Opération	Description
Valeur absolue	\(z_{k} = \|z_{k-1}\|\)
Phase (argument)	`sigima.proc.image.phase()`
Combiner avec la phase	Considère l’image courante comme le module et permet de sélectionner une image représentant la phase pour les fusionner en une image complexe `sigima.proc.image.complex_from_magnitude_phase()`
Partie réelle	\(z_{k} = \Re(z_{k-1})\)
Partie imaginaire	\(z_{k} = \Im(z_{k-1})\)
Combiner avec la partie imaginaire	Considère l’image courante comme la partie réelle et permet de sélectionner une image représentant la partie imaginaire pour les fusionner en une image complexe `sigima.proc.image.complex_from_real_imag()`

Conversion du type de données#

L’action « Convertir le type de données » permet de convertir le type de données des images sélectionnées. Pour les types de données entiers, la conversion est effectuée en rognant les valeurs à la plage de nouveaux types de données avant de convertir effectivement le type de données. Pour les types de données à virgule flottante, la conversion est directe.

Note

La conversion du type de données utilise la fonction sigima.tools.datatypes.clip_astype() qui repose sur la fonction numpy.ndarray.astype() avec les paramètres par défaut (casting=”unsafe”).

Statistiques entre les images#

Crée une nouvelle image à partir d’une opération statistique sur chaque pixel des images sélectionnées :

Opération	Description
Moyenne	\(z_{M} = \dfrac{1}{M}\sum_{k=0}^{M-1}{z_{k}}\)
Écart-type	\(z_{M} = \sqrt{\dfrac{1}{M}\sum_{k=0}^{M-1}{(y_{k} - \bar{y})^{2}}}\)
Soustraction quadratique	\(z_{2} = \dfrac{z_{1} - z_{0}}{\sqrt{2}}\)

Correction de champ plat#

Calcule la correction de champ plat à partir des deux images sélectionnées :

\[\begin{split}z_{1} = \begin{cases} \dfrac{z_{0}}{z_{f}}.\overline{z_{f}} & \text{if } z_{0} > z_{threshold} \\ z_{0} & \text{otherwise} \end{cases}`\end{split}\]

où \(z_{0}\) est l’image brute, \(z_{f}\) est l’image d’homogénéité, \(z_{threshold}\) est un seuil ajustable et \(\overline{z_{f}}\) est la valeur moyenne de l’image d’homogénéité :

\[\overline{z_{f}}= \dfrac{1}{N_{row}.N_{col}}.\sum_{i=0}^{N_{row}}\sum_{j=0}^{N_{col}}{z_{f}(i,j)}\]

Note

L’image brute et l’image d’homogénéité sont supposées avoir déjà été corrigées par soustraction d’image de noir. »n